🎶 這是好和弦的「音律的故事」系列的第 5 篇文章，總共有 6 篇。

跳到：1 | 2 | 3 | 4 | 5 | 6

在這篇文章，我要跟你說一個關於 Do-Sol 和 Do-Mi 的故事。

前情提要

在上一篇文章，我們提到了畢達哥拉斯音律系統的一個重大缺陷：「狼音程」或是「狼五度」（wolf interval 或 wolf fifth）。簡單地說就是，當使用畢達哥拉斯的調律法為鍵盤樂器調音時，音階中總會出現一個非常不和諧的完全五度。

因為狼音程的存在，作曲家們不得不避免使用某些特定的和聲組合，這限制了他們的創作範圍，使他們只能選擇特定的調與和弦，也很難任意轉調。

我們也說了，早期的音樂學家因為不知道要怎麼解決這個問題，所以就決定「不管它」。不過就算忽略狼音程的問題，畢達哥拉斯的音律還存在一個「風格上」的問題，那就是它是利用「2:3」的頻率比例，來算出新的音的。

2:3 有什麼不好嗎？

首先我們要解釋一下「2:3」這件事情。如果兩個音的頻率比例是 2:3，那麼這兩個音的關係其實就相當於現代所說的「Do 和 Sol」，我們把這樣的頻率關係叫做「完全五度」。

因為 2:3 是一個相當簡單的整數比例，所以在畢達哥拉斯音階中，Do 和 Sol 的組合聽起來特別和諧、特別穩定。

在古早古早的年代，作曲家的確是很偏好使用像是 Do-Sol 這樣的完全五度組合，所以一切都很完美。直到後來有一天，有人發現我們還可以用 Do-Mi⋯⋯

顧此（Do-Sol）失彼（Do-Mi）

如果我們把基準頻率 x 定義為 Do，根據畢達哥拉斯的方法，計算 Sol 的頻率就是將 x 乘以 3/2，得到 Sol 的頻率為 3x/2。因為 x 和 3x/2 是一個簡單的 2:3 整數比，所以這兩個音合在一起會很悅耳。

但是，畢達哥拉斯計算 Do 到 Mi 的頻率時，是將 Do 的頻率乘以 3/2 四次，然後除以 2 兩次，得出 Mi 的頻率為 81x/64。這個 64:81 的比例並不是個「簡單的」整數比，所以畢達哥拉斯的 Do 和 Mi 合在一起不是那麼好聽。

因為在 16 世紀以後的音樂，「Do-Mi」組合在音樂中的使用頻率大幅增加，這使得我們需要一個能讓「Do-Mi」聽起來更和諧的音律系統。

顧彼（Do-Mi）失此（Do-Sol）

要讓「Do-Mi」組合變好聽，必須要讓這兩個音的頻率形成一個「簡單的」整數比。畢達哥拉斯音律中的 Mi 頻率為 81x/64，嗯⋯⋯它有沒有接近哪一個簡單的分數呢？

於是就有聰明的音樂學家想到，如果把 81x/64 的 81 偷偷修改一點點，變成 80 的話⋯⋯登登！這樣就變成 80x/64，約分就是 5x/4 了，一個簡單的整數比！

所以，Mi 的頻率就這樣，幾乎沒什麼正當理由地被「指定」成 5x/4 了。

本來，在畢達哥拉斯的音律裡，如果把頻率 x 定義成 Do 的話，Mi 的計算方法是將 x 的頻率先乘以 3/2 四次，再除以 2 兩次。而現在因為 Mi 的頻率已經被指定成 5x/4，我們就不能再使用原先的「乘以 3/2」的方法來算出下一個音。

這表示，Sol 的頻率就不能再是 3x/2 了。音樂學家們為了要讓「Do-Mi」變好聽，就只好犧牲「Do-Sol」的協和程度。

那那那，原本使用了很多「Do-Sol」組合的曲子怎麼辦？那是作曲家的問題阿！微軟 Windows 改版的時候，還不是一樣有很多舊版軟體不能跑？

中庸全音律

所以後來 Sol 的頻率到底變成多高了？

如果從 Mi 的頻率 5x/4 反推，我們知道這是通過「將 x 乘以某個數字四次，再除以 4」得到的。因此，「x 乘以某個數字四次」應該等於 5x。這樣一來，「某個數字」就應該是「5 的 4 次方根」。

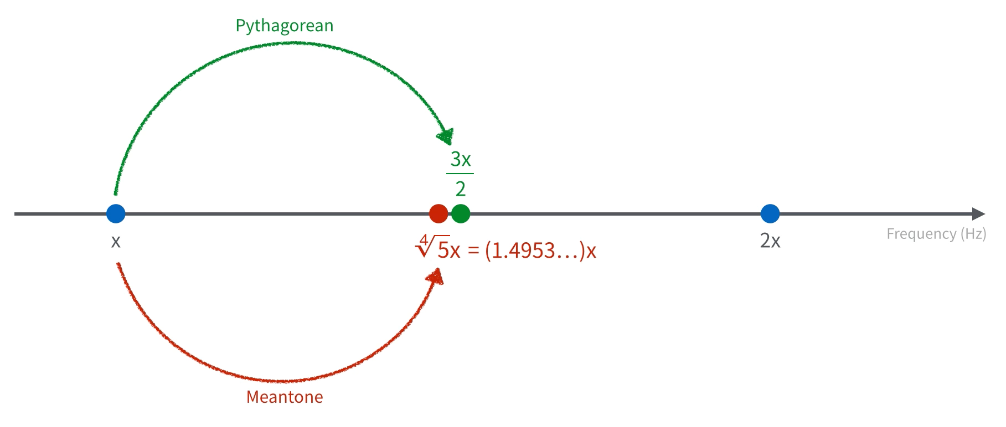
所以 Sol 的頻率變成了 ∜5x，也就是大約 1.4953x，比原本完美的 1.5x 低了一點點。

這種偏好「Do-Mi」組合的音律系統，被叫做「中庸全音律」（meantone temperament）。這個系統大概從 16 世紀初開始取代畢達哥拉斯音律，一直到大約 18 世紀初才被後續的音律系統所取代。

中庸全音律推算音高的流程與畢達哥拉斯音律完全相同，唯一的區別在於它使用「乘以 ∜5」來計算下一個高五度的音，而非畢達哥拉斯所用的「乘以 3/2」。

而且很不幸地，中庸全音律系統依然存在狼音程的問題，只是狼音出現的位置不太一樣（事實上我覺得比之前更糟），這個問題還要再過一百多年才會獲得解決。

聽聽看

最後我們來實際上聽點聲音、比較一下好了，看看你聽不聽得出這兩種音律細微的差別。

首先來聽完全五度，也就是 Do-Sol。理論上來說，畢達哥拉斯系統裡面的 Do-Sol 頻率比是 2:3 簡單整數比，應該會比較好聽；而中庸全音律是 1:1.4953，應該會稍微差一點。

我接下來會先播放畢達哥拉斯的連續三次，然後是中庸全音律的連續三次。看看你是不是有覺得前者真的有比較好聽：

接下來聽大三度，也就是 Do-Mi。畢達哥拉斯的 Do-Mi 頻率比是 64:81；而中庸全音律是完美的 4:5 簡單整數比，理論上中庸全音律應該會比較好聽。

同樣地，我會先播放畢達哥拉斯的連續三次，然後是中庸全音律的連續三次。看看你有沒有覺得後者比較好聽？

待續：怎麼總是一直不完美？

到目前為止，我們介紹過的計算音階頻率的方式，都還不是很完美；它們都會造成某些特定的音程比較協和、某些特定的音程比較難聽。所以作曲家都還是沒有辦法自由自在地使用所有的和弦，以及在曲子中任意轉調。

所以後來究竟發生了什麼突破，才讓我們得到了現代的這種，每一個調、每一個和弦都可以自由使用，也不會聽起來怪怪的調音方式呢？剩下的故事，我會在下一篇文章說完喔！

喜歡這篇文章嗎？

這篇文章也有影片版 → WiwiVideo | YouTube

如果覺得我的文章和影片對你有幫助，希望你可以藉由購買我的《鋼琴技巧急診室》和《即興幼幼班》課程、實體書、大包裝、加入頻道會員，或至少在社群媒體分享這篇文章，以實際行動來幫助好和弦的持續運作。謝謝你！

也希望你可以使用 E-mail 訂閱我，這樣才不會錯過我的最新內容喔！