🎶 這是好和弦的「音律的故事」系列的第 4 篇文章,總共有 6 篇。
前情提要
在上一篇文章,我們詳細解說了畢達哥拉斯是如何用 2:3 這個簡單的整數比,來把一個八度的頻率範圍分割成七個音。
不過你可能會問,為什麼是七個音呢?為什麼不是六個音、八個音或其他呢?好問題!
事實上,畢達哥拉斯當時的古希臘音階,其實是只有四個音的;那時候的看法,是把一個八度看成「兩個四音音階拼在一起」的組合。不過我自己對古希臘調式也不是很了解,而且老早就沒有人在用古希臘調式了,如果你有興趣的話,可以到維基百科看 Tetrachord 這篇文章,我就不要在這裡裝懂、繼續追究下去了。
總之,其實根本就沒有人知道,畢達哥拉斯到底有沒有算到第七個音。我們確定的只有,他的確是拿 2:3 這個比例為基礎來求出頻率的。
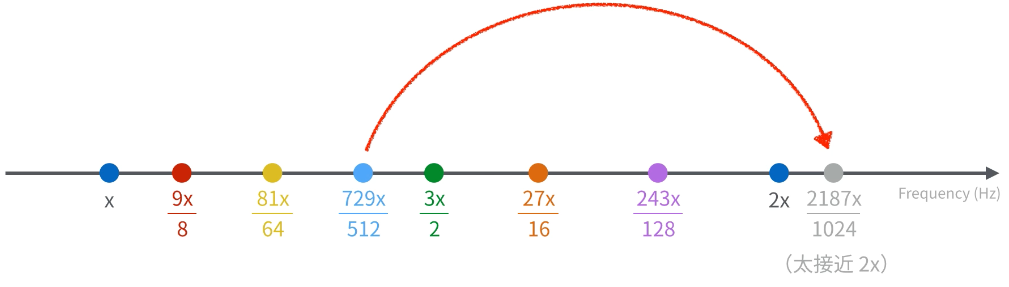
我自己的猜想是,如果繼續照著他「將頻率乘以 3/2 來求得下一個音」的方法,第七個音的頻率 729x/512 乘以 3/2 後,第八個音的頻率會變成 2187x/1024。這個數值跟 2x 有一點點太接近了,所以可能就是因為這樣,導致他覺得算到七個音就可以了吧。
不管啦,我就是想要更多音
但一千多年後的中世紀的歐洲音樂學家們,還是覺得只有七個音而已有一點太無聊,於是就想要多增加一些新的音。或者用上篇文章的說法就是:「把 x 到 2x 這個頻率範圍再細分成更多段」。
但是要怎麼做呢?當對於音階有疑問的時候,就再去問畢達哥拉斯就對了。於是,畢達哥拉斯有一天,就托夢給那時候的音樂學家說:
「將頻率乘以 3/2,如果超過 2x 的話就除以 2 ❤️」
於是剛睡醒的音樂學家們,就從畢達哥拉斯留下的第七個音 729x/512 出發:
- 729x/512 乘以 3/2 得 2187x/1024。這個數字超過 2x 了,所以除以 2,得到第八個音2187x/2048。
- 繼續將 2187x/2048 乘以 3/2,得到第九個音 6561x/4096。
- 6561x/4096 再乘以 3/2,得 19683x/8192。這個數值同樣超過 2x,因此除以 2,得到第十個音 19683x/16384。
- 接著 19683x/16384 乘以 3/2,得到第十一個音 59049x/32768。
- 59049x/32768 再乘以 3/2,得 177147x/65536。這個數值超過 2x,所以除以 2,得到第十二個音 177147x/131072。
算到這個時候,音樂學家們有一點點緊張。因為如果這個第十二個音 177147x/131072 乘以 3/2 後的第十三個音,神奇地恰好變成 2x 的話,就表示一個八度可以用 2:3 的比例完美分割成十二份,這樣畢達哥拉斯的理論就是完美的了!
所以 177147x/131072 乘以 3/2 的結果是多少呢?會不會正好是 2x 呢?答案是⋯⋯(小鼓輪奏聲)⋯⋯531441x/262144!(失望聲)
真可惜,沒有等於剛好 2x。不過如果你算一下,531441/262144 這個數字差不多是 2.027,只比 2 多出 0.027 而已,幾乎就快要是 2x 了阿!
很可能發生過的對話
然後你就可以想像,當時的音樂學家們的聚會中,可能出現了以下的對話:
音樂學家A:「真可惜,如果第 13 個音剛好等於 2x 的話就完美了!這樣一個八度就是完美地被簡單整數比 2:3 給分割成 12 個音了⋯⋯」
音樂學家B:「不過第 13 個音也離 2x 夠近了拉!你看看 531441x/262144 = 2.02728653x,才差 0.027 個八度而已阿!不如我們的音階就 12 個音就好了,這樣不是比較簡單嗎?」
音樂學家A:「可是這樣第 12 個音跟 2x 一起彈的話不是會很難聽嗎?你聽聽看其他同樣的組合都好好的⋯⋯(彈)」
音樂學家A:「可是就是這兩個音很難聽。(彈)」
音樂學家B:「還好吧!你聽⋯⋯(再聽幾次)⋯⋯誒,好像真的有點難聽耶!」
音樂學家A:「⋯⋯⋯⋯」
音樂學家B:「⋯⋯⋯⋯」
音樂學家B:「靠,管他的,反正這兩個音也很少用。」
音樂學家A:「也對,反正難聽也是作曲家的問題,干我P事!對了,你上次說啤酒很好喝的地方在哪裡?」
於是,當年歐洲中世紀的音樂學家,處理第 12 個音跟 2x 頻率合在一起不好聽的方式就是:「不管他」。
這種完全用 2:3 比例來決定音階頻率的算法,會造成一個八度裡面,有其中一個完全五度聽起來很難聽。他們那時候就真的是想說,反正又不是每一個完全五度的組合都很常用,寫曲子的人,自己避開那個很難聽的地方就好了。
或者從另一個角度來說,因為調音的人可以自由決定要把所謂的「頻率 x」設定成哪一個音,所以他可以控制那個很難聽的五度要出現在音階的哪個地方。這樣一來,只要根據演奏的曲目,把那個很難聽的五度,放在那首曲子不會用到的音那裡就可以了。
狼音程
總結來說,使用畢達哥拉斯的調律法把一個八度切成 12 個半音,必定會造成其中一個完全五度會很難聽,因為這兩個音的頻率比不是完美的 2:3,而是 177147:262144。
但是當時的音樂學家決定不管它,真的決定把這個難聽的音程組合留在音階中。這個音程後來被命名為「狼音程」或「狼五度」(wolf interval 或 wolf fifth)。它的聲音有點像之前文章和影片中提到的鋼琴走音的「抖抖」聲,至於為什麼會有人覺得這個很像是「狼」,我也不是很清楚。
「狼音程」的問題直到大約十八世紀初才稍微被解決。在那之前,作曲家寫作時必須小心避開導致狼音程的音符組合,導致他們的曲子只能寫在某些調、只能用某些和弦,也不能任意轉調。
如果你堅持要寫出會產生「狼音程」的曲子會怎樣?我接下來要彈一個小片段,先用現代正常的音律演奏一次,然後用畢達哥拉斯的音律再演奏一次,你聽聽看差別。首先是現代的音律:
然後是畢達哥拉斯的,會有很難聽的五度的音律:
待續:為什麼後來沒有狼音了?
至於為什麼更後來的音樂就沒有狼音的問題了呢?要發展成我們現代所用的音階系統,需要達成的突破是什麼?關於音律的故事還有很多可以說,趕快繼續閱讀下一篇吧!
喜歡這篇文章嗎?
這篇文章也有影片版 → WiwiVideo | YouTube
如果覺得我的文章和影片對你有幫助,希望你可以藉由購買我的《鋼琴技巧急診室》和《即興幼幼班》課程、實體書、大包裝、加入頻道會員,或至少在社群媒體分享這篇文章,以實際行動來幫助好和弦的持續運作。謝謝你!
也希望你可以使用 E-mail 訂閱我,這樣才不會錯過我的最新內容喔!