🎶 這是好和弦的「音律的故事」系列的第 3 篇文章,總共有 6 篇。
前情提要
在前面的文章中,我介紹了人耳可以聽到的頻率是 20 Hz 到 20,000 Hz。以比例來說,這個頻率範圍相當寬,因為 20 Hz 跟 20,000 Hz 相差了有 1,000 倍之遠。想要將這麼寬的頻率範圍做分割,並且將其中的頻率命名,是相當困難的事。
還好在 2,500 年前,有一位名叫畢達哥拉斯(Pythagoras)的聰明的希臘男人,發現了「八度」(Octave)這個概念。他發現,當聲音的頻率加倍或減半時,所產生的音高雖然不同,但卻又像是同一個音的不同版本;用現代用語來說,就是來到了另一個「八度」。
例如,如果我們把某個特定頻率稱為「Do」,那麼這個頻率的兩倍、四倍、八倍、十六倍、三十二倍……等等這些頻率的聲音,都會聽起來像是「Do」的不同版本。因此,這些頻率也都可以被稱為「Do」。
有了「八度」的概念,對聲音頻譜進行分割就容易多了。我們只需要選擇一個特定頻率 x,然後在 x 到 2x 的範圍內選定幾個頻率當作一些「音」。因為任何頻率只要乘以 2 或除以 2 就可以移到別的「八度」,我們就可以把在 x 到 2x 範圍內找到的音,複製到整個聲音頻譜上。
如何找到「新的音」?
OK,現在我已經選好一個頻率 x,把它叫作「Do」;然後我也知道 2x、4x、8x、16x……等等的頻率也可以就一起叫做「Do」。那接下來,要怎麼決定 Re Mi Fa Sol La Si 等等的、其他的音的頻率應該是多高呢?
如果你去問畢達哥拉斯,他八成就會回那句老話:
「宇宙萬物都可以用整數以及它們的比例來表示。」
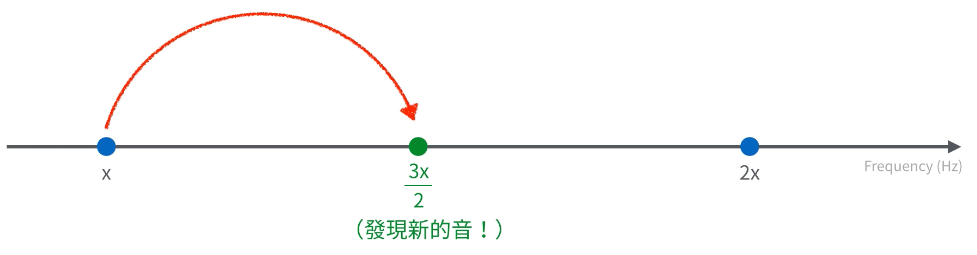
在上篇文章,畢達哥拉斯用了 1:2 的頻率比例作實驗,發現了同一個音的不同「八度」。但是只用 1:2 這個比例的話,並不能產生聽起來完全不一樣的「新的音」。於是,他決定嘗試下一個簡單的整數比例:2:3。
於是畢達哥拉斯把原本的基礎頻率 x 乘上 3/2 之後,猜猜看他找到了什麼?是「新的音」耶!我們終於有一個聽起來跟 x 頻率不一樣的音了!我接下來要用鋼琴的音色,播放 x 頻率和 3x/2 頻率給你聽:
以現代的用語來說,如果把原本的頻率 x 叫做「Do」的話,那麼 3x/2 這個頻率就相當於高完全五度的「Sol」。不過當然 2,500 年前還沒有 Do、Re、Mi、Fa、Sol 等等的名稱,我們連「音」本身在哪裡都還不知道咧,更別說是「音的名字」了。
所以畢達哥拉斯並沒有考慮這麼多,他只是在音階中找到了一個「聽起來跟頻率 x 完全不一樣的音」而已。
凡將起五音……
到這邊我要離題一下。雖然大部份西方音樂史的書,都把這種用 2:3 頻率比例來推算音階的系統,歸功給畢達哥拉斯;但其實在比畢達哥拉斯還要早一百年左右,中國春秋時代的管仲就已經想到用 2:3 頻率比例來推算音階了。
在《管子》的第 58 篇「地員篇」裡面,「凡將起五音」開始的這一段,就是地球上最早的關於用 2:3 比例來推算音階的記載,不過我中文程度太爛,不是非常看得懂他的敘述,如果你有興趣的話,自己去看看好了。
後來司馬遷的《史記》第 25 卷裡面也有寫到同樣的事情,他的敘述就好懂多了,他寫:
「九九八十一以為宮。三分去一,五十四以為徵。三分益一,七十二以為商。三分去一,四十八以為羽。三分益一,六十四以為角。」
以上翻成白話的意思就是:
- 找一個長度是 81 個單位的東西,把他的振動頻率當作 Do。
- 然後,把這個物體的長度去掉三分之一的話,就變成了剩下 54 個單位了,這個振動的頻率就當作 Sol。
- 再把這個長度是 54 的東西,增長三分之一,就變成長 72 個單位,這個就當作 Re。
- 接著把長度是 72 的 Re,再去掉三分之一,變成長 48 個單位,這個當作 La。
- 最後再把長度 48 的 La 的振動物體,增長三分之一,變成長度是 64,這個就當作 Mi。
比《管子》裡面寫得容易懂多了吧,對不對?好,結束中國這邊的話題,回到畢達哥拉斯。
畢達哥拉斯要找幾個音才高興?
畢達哥拉斯找到了頻率是 3x/2 的新的音之後,接下來就是重複同樣的步驟,再把新的音的頻率,乘上 3/2,就可以再得到一個新的音。
如果這樣操作得出的頻率超過 2x 的話,就表示這個新的音已經進到高八度的範圍了。這樣的話畢達哥拉斯就要把這個音的頻率除以 2,把它移回原來的八度。
以下是後續音高的計算過程:
- 3x/2 乘以 3/2 會得到 9x/4,而 9x/4 已經超過 2x,也就是進到更高的八度去了。於是,我們需要把這個頻率除以 2,這樣就又得到一個新的音了,頻率為 9x/8。
- 接下來,9x/8 乘以 3/2 等於 27x/16,這是下一個新音的頻率。
- 繼續這個過程,27x/16 乘以 3/2 等於 81x/32。因為又超過了 2x,我們就把它除以 2,回到原來的八度範圍,得到新音頻率為 81/64x。
- 然後再將 81x/64 乘以 3/2,得到 243x/128。
- 接著將 243x/128 乘以 3/2,得到 729x/256,這個數字超過了 2x,所以再次除以 2,得到 729x/512。
所以這個步驟是要重複幾次啊?答案是,重複到畢達哥拉斯高興為止。還好他在找到第七個不同的音,也就是 729x/512 的時候,他就覺得高興了。
這就是畢達哥拉斯的七音音階,七個音的頻率分別是: x、9x/8、81x/64、729x/512、3x/2、27x/16、243x/128。
用鋼琴的音色來演奏的話,這七個音聽起來大約像是這個樣子:
如果把它們的順序調換一下,也可以排列成這個樣子:
這聽起來幾乎就像是現代的大調音階了對不對?其實真的也滿接近的了。
待續:畢達哥拉斯調律法有什麼缺點?
畢達哥拉斯的調律法,一直被沿用到大約 1510 年左右,才被後來的中庸全音律(Meantone)調律法取代。更後來,還有被誤稱為「平均律」的 Well Temperament 調律法,最後才發展成現代通用的「等律」(Equal Temterament)。
但是為什麼畢達哥拉斯的、符合宇宙萬物運行原則、又有完美簡單整數比的調律法,後來會被取代呢?這個調律法有什麼問題?後來的為什麼比較好?期待嗎?繼續往後閱讀吧!
喜歡這篇文章嗎?
這篇文章也有影片版 → WiwiVideo | YouTube
如果覺得我的文章和影片對你有幫助,希望你可以藉由購買我的《鋼琴技巧急診室》和《即興幼幼班》課程、實體書、大包裝、加入頻道會員,或至少在社群媒體分享這篇文章,以實際行動來幫助好和弦的持續運作。謝謝你!
也希望你可以使用 E-mail 訂閱我,這樣才不會錯過我的最新內容喔!